In my 4th grade class, we have (finally) started working on division. We scrapped the "traditional" algorithm a couple of years ago in favor of the partial quotients ("Big 7") method. This has meant a LOT less tears, frustration, and hair-pullilng.... on the part of the teachers and students!
My students constantly struggle with number sense, and understanding what algorithms really mean. So, before we could dive into the Big 7 method, we had to make sure the students had a solid understanding of what division is, what the remainder represents, and have exposure to some division terms.
Bring in... the Blocks in Groups activity! You could also call this Chips in Groups, Bears in Groups, Legos in Groups... it just depends on what manipulatives you choose to use. We used unifix cubes because that's what we readily had on hand.
Here's how the activity works:
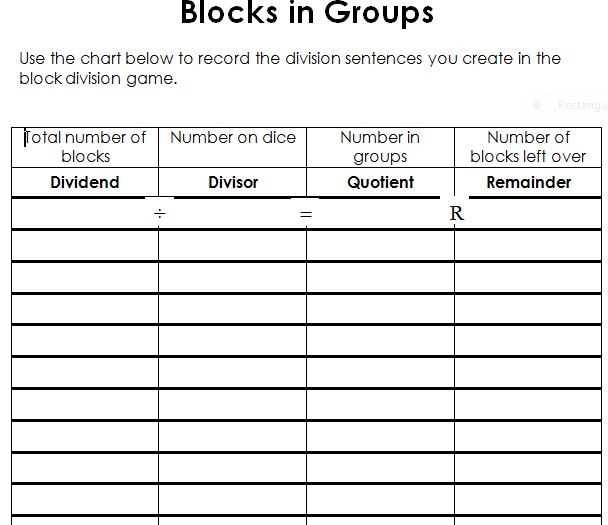
1. The student grabs a handful of cubes/blocks/chips (we'll just call them blocks from now on). The student counts the blocks and records that number in the first column. This is the dividend.
2. The student rolls a die. We used 10-sided dice, without the zero, to incorporate a larger range of numbers. Regular 6-sided dice will work just fine too. The student records the number rolled in the second column. This is the divisor.
3. The student divides the big pile of blocks into the number of groups rolled in step #2. So, if you rolled a 4 in step #2, then you would equally distribute your blocks into 4 groups. The number of blocks in each group is recorded in the third column. This is the quotient.
My co-teacher and I had an interesting discussion about this step. His "natural" way of figuring out division is to count x number (the divisor) of cubes, and see how many groups are created. My "natural" way of thinking of division is to create x number of groups, and then figure out how many cubes go in each group. We decided it's good to understand both ways, so we had our students play my way the first day, and his way the second day. This led to a great discussion about what "dividing" means.
4. The number of blocks left over is recorded in the fourth column. This is the remainder.
My students constantly struggle with number sense, and understanding what algorithms really mean. So, before we could dive into the Big 7 method, we had to make sure the students had a solid understanding of what division is, what the remainder represents, and have exposure to some division terms.
Bring in... the Blocks in Groups activity! You could also call this Chips in Groups, Bears in Groups, Legos in Groups... it just depends on what manipulatives you choose to use. We used unifix cubes because that's what we readily had on hand.
Here's how the activity works:
1. The student grabs a handful of cubes/blocks/chips (we'll just call them blocks from now on). The student counts the blocks and records that number in the first column. This is the dividend.
2. The student rolls a die. We used 10-sided dice, without the zero, to incorporate a larger range of numbers. Regular 6-sided dice will work just fine too. The student records the number rolled in the second column. This is the divisor.
3. The student divides the big pile of blocks into the number of groups rolled in step #2. So, if you rolled a 4 in step #2, then you would equally distribute your blocks into 4 groups. The number of blocks in each group is recorded in the third column. This is the quotient.
My co-teacher and I had an interesting discussion about this step. His "natural" way of figuring out division is to count x number (the divisor) of cubes, and see how many groups are created. My "natural" way of thinking of division is to create x number of groups, and then figure out how many cubes go in each group. We decided it's good to understand both ways, so we had our students play my way the first day, and his way the second day. This led to a great discussion about what "dividing" means.
4. The number of blocks left over is recorded in the fourth column. This is the remainder.
After students had a while to play, we came back together as a large group. We had the students look for any patterns they saw in their charts (ie: the remainder is always smaller than the divisor; the divisor is always smaller than the dividend; patterns when dividing by 1; etc). We even had some students who were able to describe how, mathematically, the 4 parts of the division problem fit together!
The only thing I would add to this activity is to expand it and add a writing component. To really stretch it, I would have students take one of their rows and write a story problem using those numbers. Then we would have ready-made story problems for others in the class to solve, and it would be great mathematical writing practice.
If you use this activity, I would love your feedback!
The only thing I would add to this activity is to expand it and add a writing component. To really stretch it, I would have students take one of their rows and write a story problem using those numbers. Then we would have ready-made story problems for others in the class to solve, and it would be great mathematical writing practice.
If you use this activity, I would love your feedback!

 RSS Feed
RSS Feed
